Mixture of Experts Part I

Unleashing Collective Intelligence

Imagine a future where artificial intelligence doesn't rely on a single model's intelligence but leverages multiple specialized networks. This is the promise of Mixture-of-Expert (MoE) models like Mixtral and the more recent Grok-1. Over a multi-part deep-dive series, we'll cover the basics of MoEs, some historical context, how they are trained, innovations that improved the MoE architecture and much more. 

This week, in part I, we'll delve into the motivation behind MoEs, compare them with similar models, and provide a high-level understanding of their functionality. Let's dive in.

Unleashing Collective Intelligence: Mixture of Experts - Part I

An imagination of Alan Turing’s code breakers at work. Created by DALL-E.

Too often, we credit significant breakthroughs to lone geniuses¹. However, history shows us that collaboration among specialized talents often drives innovation, from wartime cryptography to modern vaccines. 

What would this principle of collective brilliance look like if applied to AI? What if we assembled diverse expert neural networks to pool their intelligence²?

This is the core idea behind the Mixture of Experts (MoE) model: Distribute tasks to a group of expert networks, each optimized to handle a slice of the problem. This has a few benefits:

1. Efficiency: MoEs activate only the necessary experts during the forward pass, leading to faster inference speeds compared to dense networks.

2. Reduced Training Time: Only specific experts are activated for given inputs, reducing pretraining times for transformer-based MoEs.

3. Versatility: Each expert specializes in a subset of data, enabling MoEs to handle a wider variety of tasks and data types.

4. Scalability: Scaling MoEs increases capacity while limiting computation, resulting in higher data and energy efficiency³.

However, things aren't all roses—MoEs have their own challenges.

For instance, MoEs have difficulty generalizing and need the same amount of memory as a dense model. Though only a subset of experts is activated, we still need to store the entire model in memory as we don't know apriori which set of experts might be used at a given time.

We'll explore these challenges and more in a later edition. But first...

What is a Mixture-of-Experts?

At the outset, the MoE is just a neural network. An expert is simply a layer in this neural network that learns to specialize on a part of the problem. Naturally, we'll need multiple experts to address the entire problem space. Thus, the MoE has multiple copies of certain layers. Each of these copies (dubbed an expert) has its own set of parameters. 

A mixture is a combination of some of these "experts" that can best solve the example presented to the model. So, we'll need a way to choose which set of experts come together for a given example. That's where a secondary layer called the "gate" comes in. The role of the gate is to figure out which set of experts is best suited for a given input.

After reading this, you might feel that an MoE is pretty similar to some existing ML models. You’re not wrong.

Parallels with Other ML Models

Decision Trees

Both MoEs and decision trees use the divide-and-conquer strategy to manage complex tasks by breaking them into simpler sub-tasks. While decision trees follow a deterministic path, splitting data based on feature values, MoEs use a probabilistic gating network to combine outputs from multiple specialized nodes. 

Interestingly, the Hierarchical MoE proposed way back in 1994 combines decision trees and MoEs to create a tree-like structure of multiple layers of gating networks.

Ensembles

Both MoEs and ensembles combine the predictions of multiple models. However, MoEs run only one or a few expert models for each input, whereas ensemble techniques run all models on every input and then combine their outputs via averaging, stacking, and so on.

The Original MoE

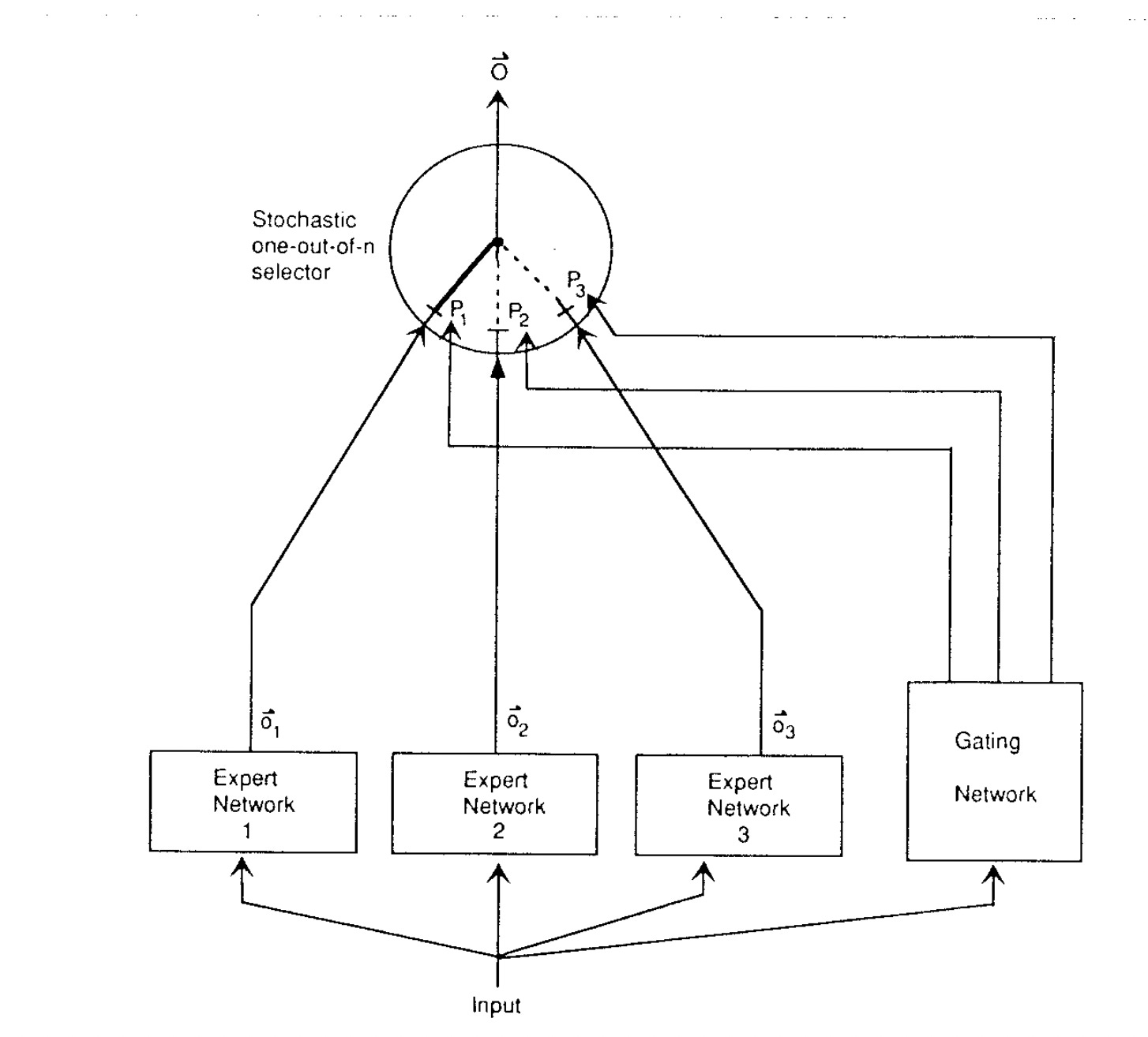
In 1991, Geoff Hinton and his collaborators first proposed MoEs as a set of feedforward networks and a gating function. In their design (shown below), all the experts received the same input. The gating function (also a feedforward network) acted as a one-out-of-n selector. It produced probability scores for each expert network, and the output of the expert with the highest probability score was selected for further processing. In their work, the experts and the gate were jointly trained to discriminate vowels⁴.

Geoff Hinton’s OG MoE. Notice that the gate is a 1-out-of-n selector. Figure taken from [1].

Here is a great video from Hinton himself explaining the intuition behind MoEs:

Innovations Few and Far Between

In the original MoE, the complete system consisted of several experts and a gating network. 

One key innovation that propelled these models further was using the MoE as a component or layer in a larger network– David Eigen and his collaborators⁵ proposed the "Deep Mixture of Experts" to do just that (in 2013). With the MoE now a layer choice, we could design larger networks that were still efficient.

The transition of the MoE from a self-contained neural network to a layer within a larger one propelled these family of models. Figure from [2] annotated by the author.

The second innovation in MoE design was conditional computation. In the original MoE, the gate determined which expert to use. However, the input was passed through all the experts and the gate before the latter made a decision.

Conditional computation determines which experts receive the input on the fly, adding further efficiency gains.

In their 2017 paper, "Outrageously Large Neural Networks:...", Noam Shazeer and collaborators explored combining these ideas at scale and tackling other challenges. The result was a 137 billion parameter LSTM model⁶ that could tackle language modeling and machine translation workloads.

The MoE layer within the outrageously large LSTM network from [4] which used conditional computing to select experts that would receive a particular input.

You might wonder why over two decades have passed since the original MoE proposal and its renaissance in the late 2010s.

The reasons are five-fold:

1. While GPUs are excellent at arithmetic, they don't shine at branching, i.e., conditional computation.

2. Performance improves with larger batch sizes. However, conditional computation within MoEs reduces batch sizes.

3. Most efforts until this point focused on image-related problems where the datasets ranged up to a few hundred thousand images. To truly test the capacity of models with billions or trillions of parameters, we need much larger datasets.

4. Network bandwidth is a major performance concern in distributed computing. The experts in an MoE are stationary, and thus, sending their inputs and outputs across the network is a communication bottleneck.

5. To tackle model quality and load-balancing (across experts), specialized loss terms are necessary.

Transformers, with their scalable architecture, thus became a suitable platform for implementing MoE layers. 

The Transformed MoE

MoEs in the context of Transformers are quite simple. We replace the feed-forward layer with a sparse MoE layer. That is, we create a set of identical feed-forward layers that are controlled by a router (a.k.a gate). Each feed-forward layer (expert) and the router have their own set of parameters. The router and experts are jointly trained. 

To ensure that the router doesn't learn to send the input to all the experts, we enforce sparsity by using the top-K function. When the router generates probability scores for each expert, we force it to select the top K highest-scoring experts to whom it should send the input⁷.

The MoE layer within a Transformer model as shown in [3]. Notice that the MoE version has half as many blocks as the original Transformer encoder.

Mathematically, the operations in an MoE layer can be explained as shown below:

The outputs from each expert (an MLP typically) are combined by the gating function. In this example, the gate is a softmax that multiples the input with its learned weights to decide which experts to use. Animation created by author.

In this first part, we learned that:

1. Mixture-of-Experts (MoE) models distribute tasks across specialized neural networks, enhancing AI efficiency and scalability.

2. MoEs offer faster inference and reduced training times, but face challenges in generalization and high memory demands.

3. MoEs can be traced back to 1991 but took over two decades to take off via modern transformer architectures.

4. MoEs use a probabilistic gating network, differing from the deterministic paths of decision trees and the full activation of ensemble methods.

5. Innovations like conditional computation in MoEs point to significant future advancements in AI model efficiency.

In the next part of this series, we’ll dive deeper into the training mechanics and innovations that make MoEs a powerful tool in modern AI. We'll explore how these models are trained, how gating networks achieve load balancing, and other cutting-edge advancements pushing the boundaries of what's possible.

References

1. Jacobs, Robert A., et al. "Adaptive mixtures of local experts." Neural computation 3.1 (1991): 79-87.

2. Eigen, David, Marc'Aurelio Ranzato, and Ilya Sutskever. "Learning factored representations in a deep mixture of experts." arXiv preprint arXiv:1312.4314 (2013).

3. Fedus, William, Barret Zoph, and Noam Shazeer. "Switch transformers: Scaling to trillion parameter models with simple and efficient sparsity." Journal of Machine Learning Research 23.120 (2022): 1-39.

4. Shazeer, Noam, et al. "Outrageously large neural networks: The sparsely-gated mixture-of-experts layer." arXiv preprint arXiv:1701.06538 (2017).

1. If I say iPhone, don't you immediately think of Steve Jobs?

2. The pooling pun is unintended. 🙂

3. Granted, dense neural networks generally improve as we increase their parameter count but this comes with its own challenges.

4. Given the complex problems we use neural nets for these days, it's always humbling to see what was considered complex a few decades back.

5. Which included one Ilya Sutskever 😉

6.  Before you say, why LSTM and not Transformers, remember that this is 2017 and Transformers weren't born yet 🙂

7. Usually K is 1 or 2 in small MoEs and 8 or more in larger models