Text-to-Image Diffusion Models Part III

From Autoencoders to Stable Diffusion -- The Finale

Jun 17, 2023

This week, we conclude the series on generative models with how diffusion models can be guided to generate what we want.

A few quick updates before we begin.

Update 1

Gradient Ascent has crossed 3000 subscribers. I'm immensely grateful for your support and kindness! When I started the newsletter, I didn't even dream of crossing this mark so soon. I thank you for your attention and time.

Update 2

Based on the voting results from last week, the next series of articles will be on language models. We'll look at a mix of old and new on this journey. Expect the first of this new series in a couple of weeks.

Update 3

This is the last month to get my book “AI for the Rest of Us” at the preorder price plus a 20% discount (use GRADASCENT at checkout) on all tiers. So, if you're on the fence, don’t miss out on the lowest pricing.

Preorder here

Let's get started!

This Week on Gradient Ascent:

An Illustrated Guide to Diffusion Models 🌬️
[Consider reading] LLMs to explore MIT's curriculum 🧠
[Consider reading] Applications of Transformers 📝
[Check out] Generative AI strategy 💪

An Illustrated Guide to Diffusion Models Contd

In our exploration of diffusion models, we've unearthed the mechanics of how they work and their underlying concepts. We've seen how these models learn to separate noise from an image. We've also journeyed through how they learn from various examples and gradually become adept at denoising pure noise to reveal the hidden picture.

But there's an elephant in the room we haven't addressed. It's a rather big elephant too. So far, we've assumed that diffusion models take a noisy image as input. That used to be the case. There's a huge problem with using images directly. Nobody wants a teeny-weeny pixelated result from these models. Everyone wants a high-resolution image that they can proudly use as a screen saver, a book cover, or pass off as their own work of art.

A high-resolution image comes with a huge computational cost. Imagine you want a 1024 by 1024 image. That's 1,048,576 pixels each with three values (one for red, green, and blue channels). Unless you're blessed with a server farm or unlimited cloud computing credits, you're not generating images that big anytime soon. You're also not training a model to produce said images anytime soon, either.

The solution to this problem is a return to latent space.

Latent Speed

One of the innovations that Stable Diffusion proposed was to compress the image first. Then, the denoising process could be done entirely on the compressed version. How do you compress an image?

Autoencoders!

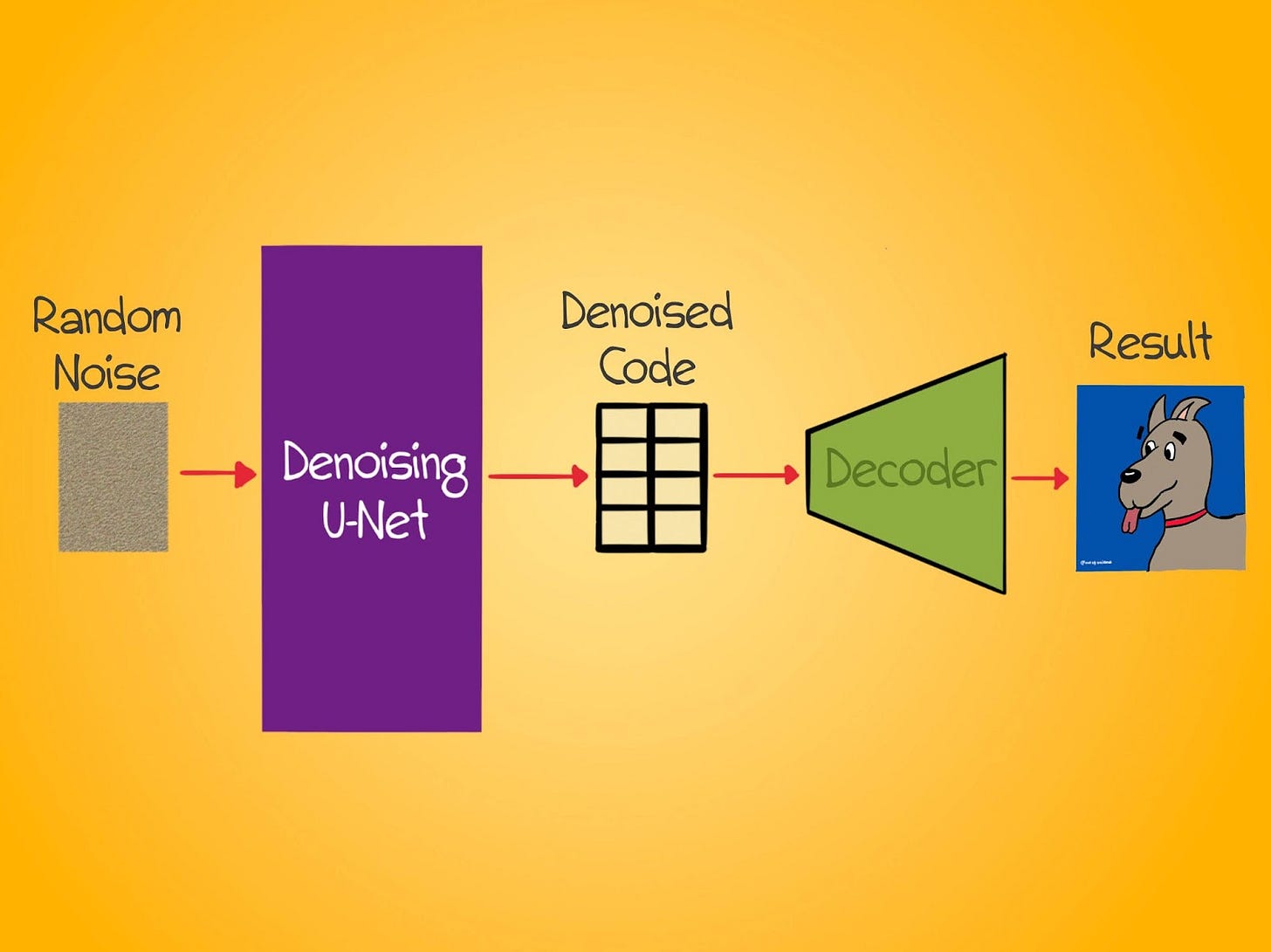
We can train an autoencoder to learn a latent representation of the images in our dataset. Great. How do we do the denoising process now? Simple. Instead of adding noise to the image, we add noise to the latent representation of the image. The U-Net that previously worked on noisy images now removes noise from noisy latent vectors. Once the latent vector is denoised, the autoencoder's decoder can reconstruct the final image using this latent vector.

This innovation is so brilliant because this small change speeds up the diffusion process by several orders of magnitude. The latent space is much, much smaller than pixel space. So it's significantly faster and more efficient to denoise in this space versus denoising in the pixel space.

So how does the training change? Not that much. The autoencoder's encoder compresses the image. We add noise to this compressed representation (a.k.a the latent vector). The U-Net now guesses what the noise is on the latent vector. We compare its guess to the actual noise added. Rinse and repeat. The autoencoder's decoder reconstructs the image from the denoised latent vector.

Once the model is trained, we can give it random noise and let the U-Net denoise it into a latent code. This code can then be fed to the decoder, which will reconstruct an image from this code.

Creating What You Want

I lied earlier. There wasn't just one elephant in the room. There were two. We've addressed one of the above. Here's the other – How do you get the model to create the images that you want? So far, our model will create images similar to what it's seen in the training data. However, we have no control over what it generates. How do we address this?

Text prompts.

In addition to giving the model random noise, we also describe what we want it to generate. This is called a prompt. The denoising U-Net can't understand text directly, so we need to feed it this information in a way that it can understand. For this, we turn to transformers.

The transformer inside diffusion models acts as a text encoder. It conveys the meaning of the prompt to the other parts of the model so that the image it generates matches the description provided. To achieve this, the transformer is trained with a dataset containing both images and captions. Each caption describes what the image is. In practice, these datasets are images scraped from the web along with their alt tags. That's why all the prompts we write don't read like conversational text but rather like cryptic shorthand.

Armed with these pairs of images and text, we can teach the transformer to produce special text embeddings. Here's how. Say we have an image of a cow in a field. The caption that's associated with it reads, "Cow grazing in a field; sunshine; meadow." We ask the transformer to produce two sets of embeddings. One for the image of the cow in the field and another for the caption. Now, we can take another caption that is completely unrelated to the image – "An astronaut taking a coffee break on the moon." We can ask our transformer to produce a text embedding for this caption as well.

We now have an image embedding and two text embeddings. One of these text embeddings matches the image closely, while the other does not. Using a technique called contrastive learning, we can train the transformer to bring the correct pair of image and text embeddings closer together and push the incorrect pair of image and text embeddings far apart.

How does it work?

We play a "match the pairs" game with the transformer, where each image-text duo is a pair. A positive pair corresponds to the image and its correct caption (related text), and a negative pair consists of the image and an irrelevant caption (unrelated text). For every such pair, we ask the transformer to decide whether the text matches the image. We then compare its guess with the actual label. If the guess is correct, the loss function decreases; if it's wrong, the loss function increases, providing a learning opportunity. Iterating this process refines the transformer's ability to produce accurate text embeddings that align with image embeddings.

If we do this for a large number of image-text pairs, the transformer learns the correct "text" representation of an image.

Thus contrastive learning brings similar things together and pushes dissimilar things apart.

Once this transformer has been trained, we can feed it prompts, and it will produce a text embedding that best represents the prompt. Our denoising U-Net can understand embeddings. Huzzah!

So now, we can feed the U-Net a text embedding that represents the prompt and a random noise vector. The U-Net learns to use this text embedding to guide noise removal. Returning to our cats and dogs example from last time, we'd now give a prompt like "Spotted cat sitting on a couch" along with a noisy latent vector. The denoiser would think, "Hmm, I need to remove noise so that what remains is a spotted cat on a couch."

This helps it generate an image that we want versus a random image. Thus, end-to-end, we provide a text prompt and receive an image matching the prompt. Internally, the prompt is converted to a text embedding. This, along with a noisy latent vector, is fed to the denoiser. The denoiser produces a denoised latent vector which the autoencoder's decoder reconstructs into a beautiful image.

In practice, there's a lot more nuance and details to how these models work, but what we've covered so far captures the main ideas behind how they can generate incredible imagery. As these models get better and as the training data improves, the capabilities of these models will improve significantly, leading to a seismic shift in various creative media. Game developers, designers, and other creative professionals will be able to increase their productivity and their project scope significantly. Creatives will only be limited by their imagination.

I hope you enjoyed this series on generative models. We're looking at language models next.

Resources To Consider:

LLMs explore MIT's Math & EECS Curriculum

Paper: https://arxiv.org/abs//2306.08997

In this paper, researchers curated a dataset of 4550 questions and answers from across MIT's mathematics and EECS courses. They then evaluated whether LLMs fulfill the graduation requirements based on their performance on these questions. The results are very interesting and somewhat eye-opening on the state of curriculum design and tests.

Applications of Transformers

Paper: https://arxiv.org/abs/2306.07303

This comprehensive survey paper covers the wide-ranging applications of Transformers across various domains, including computer vision, audio, speech, healthcare, and IoT. This is worth checking out to get a solid grounding on what Transformers are being used for and the broader implications of this technology.

Generative AI Strategy

Link: https://huyenchip.com/2023/06/07/generative-ai-strategy.html

Chip Huyen recently presented a wonderful talk on Generative AI strategy at a conference. The talk itself doesn't seem to have been recorded, but the slides are available above. Consider reading this to get an idea of how you can leverage generative models.